Notre système solaire est composé d'une étoile, le Soleil, et de tous les objets célestes gravitant autour de lui : les huit planètes confirmées et leurs 185 satellites naturels, les cinq planètes naines et leurs neuf satellites naturels connus et les milliards de petits corps (la grande majorité des astéroïdes et autres planètes mineurs, les comètes, les poussières interplanétaires, etc...
De façon schématique, le Système solaire est composé, outre le Soleil lui-même et par ordre de distance croissante à celui-ci, de quatre planètes telluriques internes (Mercure, Vénus, la Terre et Mars), d'une ceinture d'astéroïdes composée de petits corps rocheux, de quatre planètes géantes externes (deux géantes gazeuses que sont Jupiter et Saturne, et deux planètes géantes de glaces que sont Uranus et Neptune) et de la ceinture de Kuiper, composée elle-même d’objets glacés. L'héliopause, limite magnétique du Système solaire, est définie par l'arrêt des vents solaires face au vent galactique. Bien au-delà se trouve le nuage d'Oort, sphère d’objets épars. La limite gravitationnelle du Système solaire se situe bien plus loin encore, jusqu'à 1 ou 2 années-lumière du Soleil.
Source : Wikipédia

D'après la première loi de Képler, les planètes du système solaire décrivent des trajectoires elliptiques, dont le Soleil occupe l'un des foyers comme par exemple pour la planète Mercure dont l'orbite est représentée ci-dessous :
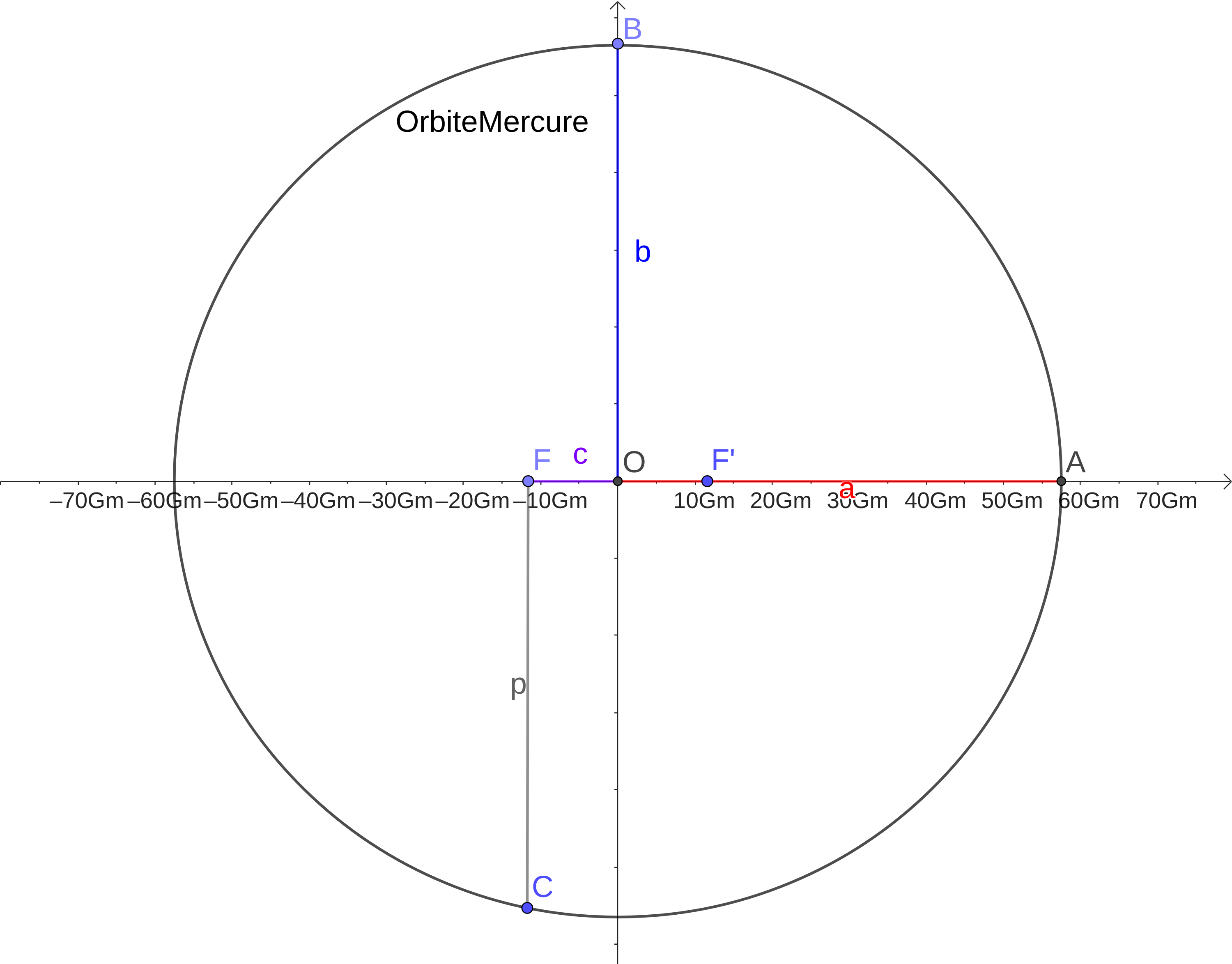
1. Créer un script permettant, à l'aide de pocketgl, d'afficher une fenêtre (appelée systeme solaire reduit) de dimensions 800x600 pixels ainsi qu'un système d'axes orthogonaux centré sur le point (400,300).
2. Définir une fonction trace_orbite(a,e) permettant, à l'aide du demi-grand axe a et de l'excentricité e de l'orbite elliptique, de tracer dans cette fenêtre une orbite. Utiliser cette fonction pour tracer à l'aide du script précédent l'orbite de la Terre en utilisant comme échelle 1 pixel pour 1 million de km.
Données : pour la Terre, a=150 millions de km et e=0,017
Aide : pour un point M de l'ellipse, les coordonnées x et y d'un point vérifient les relations y=((b**2)*(1-x**2/a**2))**(1/2) ou y=-((b**2)*(1-x**2/a**2))**(1/2)
Un exemple d'exécution :
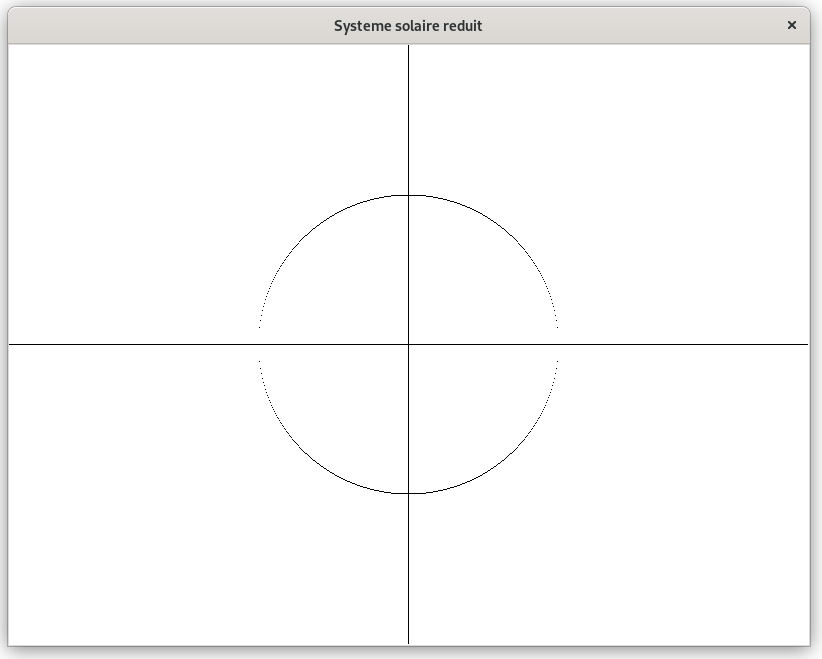
3. Modifier votre programme pour qu'il affiche les orbites des quatre planètes telluriques, dont les noms et les paramètres orbitaux sont contenus dans les listes suivantes :
nom=["Mercure","Vénus","Terre", "Mars"]
excentricite=[0.206,0.007,0.017,0.093]
demigrandaxe=[58,108,150,228]
4. Il est possible d'afficher du texte à l'aide de pocketgl en utilisant la fonction text(px,py,pch) où pch est le teste à afficher et (px,py) les coordonnées de la position d'alignement à gauche. Modifier votre script pour que les noms des 4 planètes apparaissent à côté de leurs orbites.
Un exemple d'exécution :
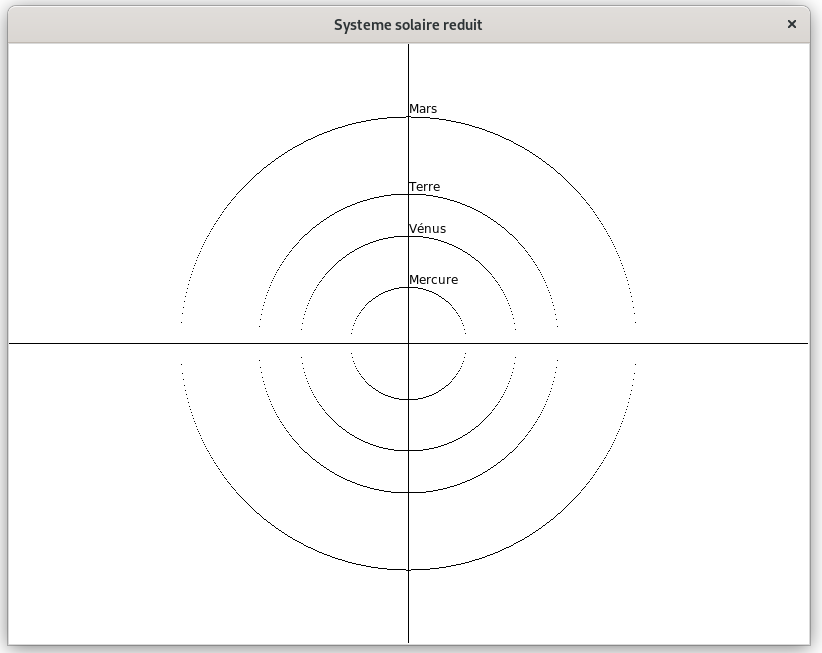

Nous allons appliquer dans cet exercice la méthode d'Euler pour prévoir la position de la Terre dans l'espace à la date t+1 jour connaissant la position, la vitesse et l'accélération à la date t. On négligera l'influence gravitationnelle des différents astres du système solaire à l'exception du Soleil.
1. Reprendre le script précédent permettant, à l'aide de pocketgl, d'afficher une fenêtre de dimensions 800x600 pixels, un système d'axes orthogonaux centré sur le point (400,300). Y ajouter la position de la Terre représentée par un disque bleu de rayon 10 pixels au périhélie.
2. Représenter la position du Soleil sous la forme d'un disque jaune de rayon 20 pixels sachant qu'au périhélie la distance Terre-Soleil vaut environ 147 millions de km.
3. Définir une fonction Euler(G,dG,dt) permettant, à l'aide de la valeur G d'une grandeur à l'instant t, de celle de sa dérivée dG et d'un pas dt, d'obtenir par la méthode d'Euler la valeur de G à l'instant t+dt.
Un exemple d'exécution :
Euler(30,2,1)
32
4. Définir une fonction Distance(x,y,xS,yS) retournant la valeur, en millions de km, de la distance r entre une planète de coordonnées (x,y) et le Soleil de coordonnées (xS,yS).
Un exemple d'exécution :
Distance(550,300,407,300)
143.0
5. Définir une fonction Acceleration(r) retournant la valeur, en millions de km.j-2, de l'accélération a d'une planète située à la distance r du Soleil sous l'influence de la force gravitationnelle exercée par le Soleil.
Aide : la valeur de l'accélération, découlant de l'application du PFD à une planète du système solaire est a=G*mS/r**2 où G est la constante de la gravitation valant 6.67E-11 S.I. et mS la masse du Soleil valant 1.99E30 kg.
Un exemple d'exécution :
Acceleration(147)
0.04585341920866306
6. Définir une fonction Ax_heliocentrique(x,y,xS,yS) permettant de calculer la composante Ax de l'accélération d'une planète dans le référentiel héliocentrique.
Aide : la composante Ax se calcule à l'aide des positions x et xS de la planète et du Soleil, de la distance planète-Soleil r et de la valeur de l'accélération a grâce à l'expression Ax=-a*(x-xS)/r.
Un exemple d'exécution :
Ax_heliocentrique(550,300,407,300)
-0.04845452274830065
7. Définir de même une fonction Ay_heliocentrique(x,y,xS,yS) permettant de calculer la composante Ay de l'accélération de la planète dans le référentiel héliocentrique.
Un exemple d'exécution :
Ay_heliocentrique(550,300,407,300)
-0.0
8. Modifier votre script pour représenter les positions de la Terre, calculées à l'aide de la méthode d'Euler, en prenant comme origine des temps la date du périhélie en 2017, soit le 4/01/2017, pour lequel la Terre avait comme composantes de vitesse orbitale vy = 2.6167968 millions de km par jour et vx=0 et comme position dans le repère choisi (554,300). On choisira comme pas du calcul 1 jour.
Aide 1 : pour générer l'animation, il faut insérer le code d'affichage compris entre les instructions init_window() et main_loop() dans une boucle while infinie puis utiliser les fonctions sleep(), refresh() et clear_screen(). Par exemple :
init_window ("Systeme solaire reduit",800,600)
while True :
........insérer ici le code d'affichage...
.....refresh()
.....sleep(0.05)
.....clear_screen()
main_loop ()
9. Superposer à l'animation du mouvement de la Terre la trace de l'orbite terrestre: utiliser pour cela la fonction trace_orbite(a,e) de l'exercice précédent. On prendra a = 150 (en millions de km) et e = 0.01671022 pour la Terre.
10. Modifier votre script pour afficher aussi les positions de Mercure sous la forme d'un disque gris de rayon 4 px, Vénus sous la forme d'un disque orange de rayon 10 px et Mars sous la forme d'un disque rouge de rayon 5 px. On donne les listes suivantes contenant les informations nécessaire au tracé des ellipses et à l'application de la méthode d'Euler pour toutes ces planètes à partir du 4/01/2017 :
nom=["Mercure","Vénus","Terre", "Mars"]
e=[0.20563069,0.0068,0.01671022,0.09341233]
a=[58,108,150,229]
x=[450,478,554,423]
y=[325,218,300,89]
vx=[-2.4070574,2.29260285,0,2.24824215]
vy=[4.12331415,1.98626515,2.6167968,0.172993]
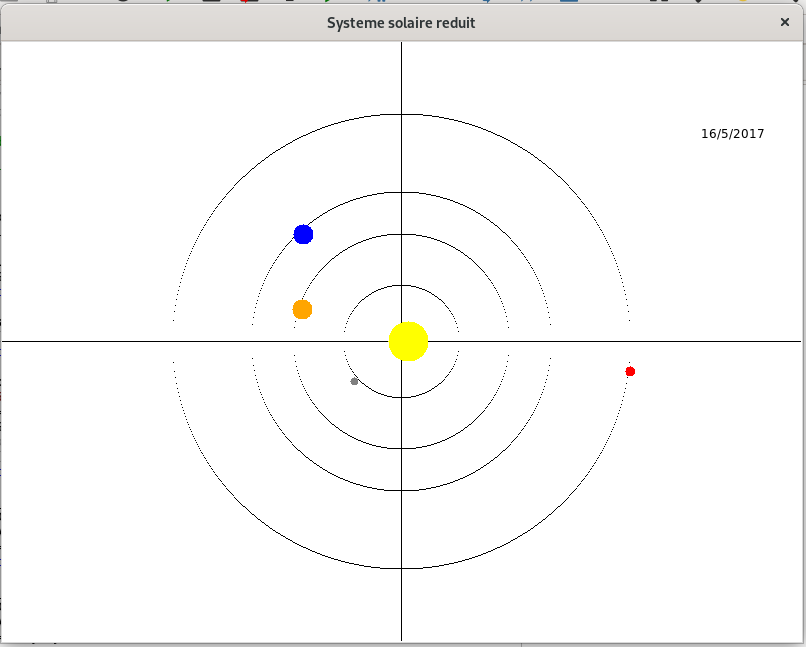
11. Définir une fonction change_date(date) qui à partir d'une liste date=[jour,moi,annee] ajoute un jour à cette date, en tenant compte du nombre réel de jours par mois ainsi que des années bissextiles. Afficher et mettre à jour en permanence cette date à l'écran à l'aide de la fonction text(px, py, pch).
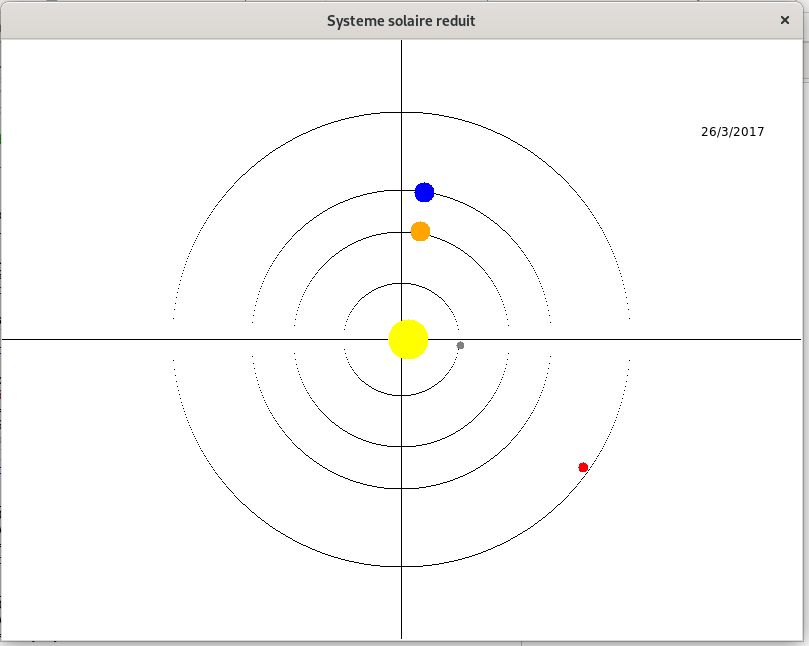
Voici un aperçu de ce que vous devez obtenir :
 ....
....
 ....
....