


Les structures de contrôle permettent, en programmation, d'influencer le déroulement d'un programme que ce soit en opérant un choix entre plusieurs options possibles ou en répétant plusieurs fois une section d'un programme jusqu'à ce qu'une condition fixée au préalable soit réalisée.
La sélection est une structure de contrôle, c'est à dire un groupe d'instructions qui déterminent l'ordre dans lequel les actions sont effectuées. Elle permet d'orienter le déroulement du programme dans différentes directions en fonction des circonstances rencontrées.
if est la plus simple des instructions conditionnelles : elle permet de tester une condition et de n'exécuter les instructions que si cette condition est vérifiée.
Un exemple :
note = 8
if note < 10 :
.....print("Vous n'avez pas eu la moyenne")
En exécutant ce programme, on voit s'afficher à l'écran "Vous n'avez pas eu la moyenne".
On peut améliorer le programme pour prendre en compte le cas où "note" est plus grande que dix à l'aide de l'instruction else:
if note < 10 :
.....print("Vous n'avez pas eu la moyenne")
else :
.....print("Vous avez eu la moyenne")
On utilise aussi parfois elif (contraction de "else if") :
if note < 10 :
.....print("Vous n'avez pas eu la moyenne")
elif note == 10 :
.....print("Vous avez eu pile la moyenne")
else :
.....print("Vous avez eu plus de la moyenne")

1. Écrire un script qui demande à l’utilisateur une note sur 20 et affiche s’il a réussi ou non l’examen selon que sa note est supérieure à 10 ou non. De plus si la note est supérieure à 12, 14 ou 16, le programme affichera la mention correspondante.
2. Écrire un script qui demande trois notes d’UE à l’utilisateur. Le programme affichera semestre valide si la moyenne des notes est supérieure à 10, il rajoutera par compensation si une ou plusieurs notes sont inférieures à 10, sinon il affichera session de rattrapage.

Le but de l'exercice est d'écrire un script permettant de déterminer la ou les solutions réelles (si elles existent) d'une équation du second degré. L'équation du second degré étudiée est supposée être sous la forme a x² + b x + c =0.
1. Créer un script affichant la ou les solutions réelles (si elles existent) prenant en compte les valeurs des trois paramètres a, b, c saisis par l'utilisateur. Votre script devra prendre en compte la valeur particulière c=0.
Remarque : il est possible en python de calculer la racine carré d'un nombre sans avoir recours à la bibliothèque de fonctions math grâce à la puissance ½.



1. Écrire un script permettant d’effectuer des opérations entre deux nombres entiers entrés au clavier. L’utilisateur devra entrer successivement l’entier a, l’opérateur op à choisir parmi +, -, *, / et l’entier b.
2. Améliorer l’affichage pour obtenir en sortie par exemple :
Entrez l'entier a : 1
Entrez l'operateur op : /
Entrez l'entier b : 2
Le resultat est 1 / 2 = 0.5
Cette expression est de type class 'float'

La répétition est aussi une structure de contrôle. Elle permet de répéter un certain nombre de fois une instruction donnée ou un bloc d'instructions. L'instruction while en est un exemple : elle permet de répéter plusieurs fois un bloc d'instructions (en boucle) tant qu'une ou plusieurs conditions sont vraies.
Par exemple le code :
i = 0
while i < 5:
.....print(i)
.....i = i + 1
donne à l'exécution : 0 1 2 3 4
L'autre exemple est l'instruction for : elle permet d'exécuter une itération un certain nombre de fois. On peut par exemple obtenir le même résultat à l'exécution que précédemment à l'aide du code suivant :
for i in range(5):
.....print(i)
On peut en particulier spécifier à une boucle for la valeur de départ des itérations :
for i in range(2,5):
.....print(i)
ce qui donne à l'exécution : 2 3 4
Une boucle for peut aussi être arrêtée avant sa fin grâce à l'instruction "break", comme dans le code suivant :
for i in range(5):
.....if i==3:
..........break
.....print(i)
qui donne à l'exécution : 0 1 2

Modifier le script de l'exercice 3 pour qu’il relance la calculatrice selon que l’utilisateur lui signale ’y’ pour continuer ou ’n’ pour s’arrêter.

La série de Lyman correspond à toutes les transitions électroniques des états excités (n ≥ 2) de l'atome d'hydrogène vers son état fondamental (n = 1) et se traduit par l'émission d'une série de raies spectrales dans l'ultraviolet (n est le nombre quantique principal désignant le niveau d’énergie de l'électron). Ces raies furent découvertes par Théodore Lyman entre 1906 et 1914. C'est le physicien suédois Johannes Rydberg qui avait prévu en 1888 l'existence de ces raies à l'aide d'une formule empirique de son cru :
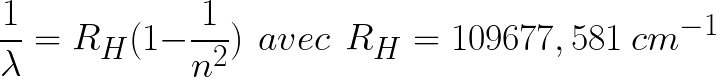
où n est un entier naturel supérieur ou égal à 2 et RH la constante de Rydberg de l'hydrogène.
Ecrire un script qui affiche les longueurs d'onde en nm à 0,01 nm près (arrondi à l'inférieur) des 8 premières raies de Lyman comme suit.
Rappel : 1 nanomètre ou nm correspond à 10**(-9) m
Un exemple d'exécution :
Les 8 premieres raies de Lyman
La raie n° 1 de Lyman a pour longueur d'onde 121.56 nm
La raie n° 2 de Lyman a pour longueur d'onde 102.57 nm
La raie n° 3 de Lyman a pour longueur d'onde 97.25 nm
La raie n° 4 de Lyman a pour longueur d'onde 94.97 nm
La raie n° 5 de Lyman a pour longueur d'onde 93.78 nm
La raie n° 6 de Lyman a pour longueur d'onde 93.07 nm
La raie n° 7 de Lyman a pour longueur d'onde 92.62 nm
La raie n° 8 de Lyman a pour longueur d'onde 92.31 nm

D'autres séries de raies spectrales existent pour l'hydrogène, dont la longueur d'onde peut être calculée à l'aide de la formule suivante, issue du modèle établi par Rydberg :
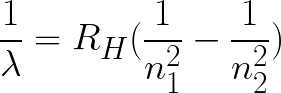
Dans cette formule, n1 et n2 désignent les niveaux d'énergie (n2 > n1).
On obtient la série de Lyman en faisant n1=1, celle de Balmer avec n1=2, de Paschen avec n1=3, de Brackett avec n1=4, de Pfund avec n1=5 et on obtient celle d'Humphreys avec n1=6.
Ecrire un script qui calcule et affiche les 8 premières raies des séries de Lyman, Balmer, Paschen, Brackett, Pfund et Humphreys comme suit :
Les 8 premieres raies de Lyman
121.56 nm 102.57 nm 97.25 nm 94.97 nm 93.78 nm 93.07 nm 92.62 nm 92.31 nm
Les 8 premieres raies de Balmer
656.46 nm 486.27 nm 434.17 nm 410.29 nm 397.12 nm 389.01 nm 383.65 nm 379.9 nm
Les 8 premieres raies de Paschen
1875.62 nm 1282.16 nm 1094.11 nm 1005.21 nm 954.86 nm 923.16 nm 901.74 nm 886.52 nm
Les 8 premieres raies de Brackett
4052.28 nm 2625.87 nm 2166.12 nm 1945.09 nm 1817.91 nm 1736.69 nm 1681.11 nm 1641.17 nm
Les 8 premieres raies de Pfund
7459.88 nm 4653.79 nm 3740.56 nm 3297.0 nm 3039.21 nm 2873.0 nm 2758.27 nm 2675.13 nm
Les 8 premieres raies de Humphreys
12371.92 nm 7502.5 nm 5908.22 nm 5128.66 nm 4672.51 nm 4376.46 nm 4170.8 nm 4020.87 nm

Ecrire un script permettant d'afficher sur 8 caractères un nombre binaire possédant au plus 8 bits.
Des exemples d'exécution :
Entrez votre nombre binaire codé sur au plus 8 bits : 101
Le nombre binaire codé sur 8 bits est : 00000101
Entrez votre nombre binaire codé sur au plus 8 bits : 100110
Le nombre binaire codé sur 8 bits est : 00100110
Entrez votre nombre binaire codé sur au plus 8 bits : 11001010
Le nombre binaire codé sur 8 bits est : 11001010

La méthode d'Euler, nommée ainsi en l'honneur du mathématicien Leonhard Euler, est une procédure numérique itérative pour résoudre par approximation des équations différentielles. Dans sa version semi-explicite, elle peut être utilisée en mécanique Newtonienne pour résoudre certains problèmes.
Principes de la méthode :
Application à un cas simple : Mouvement vertical dans un champ de pesanteur
Nous allons appliquer la méthode d'Euler pour déterminer la hauteur maximale atteinte par une boule lancée vers le haut à l'instant t=0 avec une vitesse v0 depuis l'altitude z=0 (l'axe Oz vertical est choisi orienté vers le haut). On supposera dans un premier temps que la force de frottements de l'air est négligeable.
Par application du PFD, il vient : a = Cte = -g = -9.81 m/s2
La vitesse à l'instant t+dt s'exprime alors par : v(t+dt)=v(t)-g*dt
L'altitude z à l'instant t+dt par : z(t+dt)=z(t)+v(t+dt)*dt
1. Ecrire un script permettant à l'aide d'une vitesse intiale v0 et d'un pas du calcul dt saisi par l'utilisateur, de déterminer l'altitude maximale atteinte par la boule.
Rappel : lorsque la boule atteint son altitude maximale, sa vitesse change de signe (positive car selon l'axe Oz lors de la montée, elle devient négative lors de la descente).
Un exemple d'exécution :
Entrez la valeur de la vitesse en m/s : 15
Entrez le pas du calcul : 0.0001
L'altitude maximum atteinte par la boule est : 11.467139920503792 m
2. Dans certaines conditions on peut admettre que la force de frottement qui s'exerce sur l'objet est de la forme F = - k*v, où k représente le coefficient de résistance de l'objet (la boule) dans le fluide en question (ici l'air).
Dans ce cas, l'accélération n'est plus constante mais dépend de la vitesse de la boule : m*a = - m*g - k*v
ce qui donne pour l'expression de l'accélération à l'instant t+dt : a(t+dt)=-g-(k/m)*v(t)
Modifier le script précédent pour prendre en compte la saisie utilisateur de la masse de l'objet, de son coefficient de résistance ainsi que de la nouvelle expression de son accélération.
Un exemple d'exécution :
Entrez la valeur de la vitesse en m/s : 15
Entrez le pas du calcul : 0.001
Entrez la masse de la boule en kg : 0.690
Entrez le coefficient de resistance en kg/s : 0.049
L'altitude maximum atteinte par la boule est : 10.692072287935144 m
3. Lorsque la vitesse devient importante, l'écoulement de l'air autour de la boule devient turbulent et la force de frottement qui s'exerce sur elle est plutôt de la forme F = - k*v².
L'équation vérifiée par l'accélération est alors dans ce cas : m*a = - m*g - k*v²
ce qui donne pour l'expression de l'accélération à l'instant t+dt : a(t+dt)=-g-(k/m)*v(t)²
Modifier le script précédent en prenant en compte cette nouvelle expression de l'accélération.
Un exemple d'exécution :
Entrez la valeur de la vitesse en m/s : 15
Entrez le pas du calcul : 0.001
Entrez la masse de la boule : 0.690
Entrez le coefficient de resistance en kg/s : 0.049
L'altitude maximum atteinte par la boule est : 6.793219549674259 m
4. Modifier le script précédent de manière à ce que le pas du calcul, initialement fixé à 0.1, soit automatiquement ajusté pour que la précision du résultat obtenu soit inférieure à une précision saisie par l'utilisateur. Le programme affichera en plus du résultat la valeur du pas du calcul ainsi que le nombre d'itérations effectuées pour obtenir ce résultat.
Un exemple d'exécution :
Entrez la valeur de la vitesse en m/s : 15
Entrez la masse de la boule en kg : 0.690
Entrez le coefficient de resistance en kg/s : 0.049
Entrez la précision souhaitée : 0.01
L'altitude maximum atteinte par la boule est : 6.804950950567434 m
Le pas utilise a ete de : 1e-5
Le resultat a ete atteint en 120630 iterations