On peut faire appel à différentes bibliothèques sous python pour générer et afficher des graphismes 2D. Dans les exercices suivants, on fera appel au module pocketgl :
# PocketGL - Pocket Graphics Library
# Version 1.0 (19 mai 2016)
# module graphique minimaliste
# Christian NGUYEN - nguyen@univ-tln.fr
# http://nguyen.univ-tln.fr
Ce dernier propose quelques fonctions qui simplifient le travail du programmeur qui souhaite avoir une sortie graphique 2D. Il est téléchargeable à l'adresse suivante ICI. Vous devez enregistrer ce module dans le même dossier que votre programme pour que celui-ci puisse importer toutes les fonctions qu'il contient à l'aide de la ligne suivante :
from pocketgl import *
Il comporte notamment les fonctions suivantes :

1. Taper dans l'éditeur python le script suivant puis l'exécuter. En déduire la significations des arguments des fonctions point(px,py), box(px1,py1,px2,py2), circle(px,py,pr,pep=1), line(px1,py1,px2,py2,pep=1)
from pocketgl import *
init_window ("premiers pas",400,400)
point(400,400)
point(402,400)
current_color("blue")
box(0,0,50,100)
current_color("red")
circle(250,250,40,3)
current_color(0,255,0)
line(50,50,200,100,2)
main_loop ()
2. Écrire un programme qui affiche une fenêtre de 500x500 pixels et la remplit de barres horizontales de 10 pixels de large en dégradé de gris.
Un exemple d'exécution :

Le but de l'exercice est d'écrire un script python permettant de représenter de la bonne couleur la figure obtenue lors de la diffraction de la lumière par une fente. Pour cela nous aurons besoin d'un rendu colorimétrique, c'est à dire d'une méthode permettant de transcrire une couleur en un triplet de valeurs RVB comprises entre 0 et 255 qui pourra être utilisé par pocketgl pour représenter la courbe et la figure de diffraction de la bonne couleur .
1. A l'aide du tableau suivant, créez un script contenant la liste L ordonnée des longueurs d'onde limites en m des domaines colorés ci-dessous.
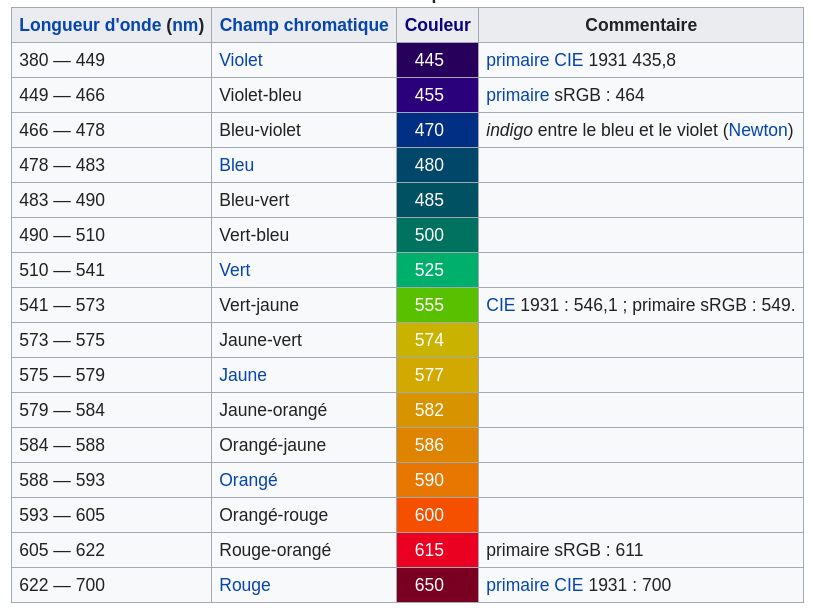
2. Ajouter la liste de couleurs color suivante, contenant les tuples (R,V,B) associés à chaque couleur.
color=[(15,0,36),(17,0,48),(0,18,51),(0,28,41),(0,32,38),(0,45,37),(0,69,42),(35,75,0),(79,70,0),(82,66,0),(84,58,0),(87,52,0), (91,47,0),(96,31,0),(92,0,13),(48,0,13)]
3. Reprendre le programme réalisé dans le TP précédent permettant de tracer la courbe représentant l'intensité lumineuse en fonction de l'abscisse du point M. Le modifier pour afficher, à l'aide de pocketgl et en utilisant la bonne couleur, la courbe dans une fenêtre de dimensions 500x500 pixels en utilisant 500 points.
Remarque : on utilisera le numéro du pixel comme abscisse pour placer un point dans la fenêtre car on ne peut pas afficher plus d'abscisses différentes qu'il y a de pixels sur une largeur de fenêtre. Il faudra par contre calculer la valeur de l'abscisse du point M pour calculer l'intensité lumineuse en ce point.
Un exemple d'exécution :

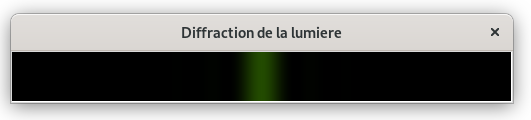
4. Modifier le programme précédent pour afficher la figure de diffraction obtenue dans une fenêtre de dimensions 500x50 pixels.
Aide : on affichera cette fois-ci une série de lignes verticales dont la valeur des composantes RVB de la couleur sera pondérée par la valeur de l'intensité lumineuse.
Un exemple d'exécution :

Un prisme est un bloc de verre taillé, composé classiquement de trois faces sur une base triangulaire. Il était utilisé dès l'antiquité pour son côté esthétique ou pour décomposer la lumière. C'est Isaac Newton, au XVIII ème siècle, qui l'intégra dans un dispositif expérimental destiné à mieux comprendre la nature de la lumière. Depuis, les prismes sont utilisés en spectroscopie et dans toute application nécessitant des déviations ou des séparations de faisceau.
L'indice de réfraction d'un prisme dépend de la longueur d'onde et peut-être déduit de l'équation de Sellmeier :
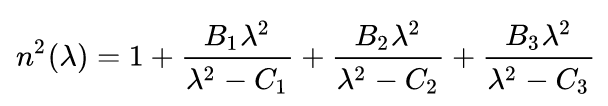
Pour un verre de type BK7 couramment utilisé en spectroscopie, la liste des coefficients de Sellmeier est la suivante :
B1=1.03961212
B2=0.231792344
B3=1.01046945
C1=0.00600069867
C2=0.0200179144
C3=103.560653
1. Définir une fonction indice(lo) retournant la valeur de l'indice n d'un prisme fabriqué à partir de verre BK7, les valeurs des coefficients de Sellmeier étant initialisés dans la fonction.
Attention : les longueurs d'onde doivent être exprimées en µm dans la relation de Sellmeier.
Un exemple d'exécution :
>>> indice(1.004)
1.5074463569455943
2. L'angle déviation au minimum de déviation d'un rayon lumineux par un prisme est donné par la formule : Dm=(n-1)*A où Dm est l'angle de déviation au minimum de déviation, n l'indice du prisme pour la longueur d'onde sélectionnée et A l'angle au sommet du prisme.
Définir une fonction deviation(lo,A) utilisant la longueur d'onde lo exprimée en µm et l'angle au sommet A du prisme exprimé en ° retournant la valeur de l'angle de déviation Dm.
Un exemple d'exécution :
>>> deviation(0.38,30)
16.012345977756972
3. Définir une fonction position(lo,A,D) retournant la position x du rayon de longueur d'onde lo exprimée en µm dévié sur un écran situé à une grande distance D du prisme. On considérera en première approximation que tan(Dm)=Dm=x/D avec Dm exprimée en radians, x et D exprimée en m.
Un exemple d'exécution :
>>> position(0.38,30,3)
0.8384044748409897
4. Définir une fonction px(L,A,D) retournant la liste des valeurs des positions px dans une fenêtre de 500x500 pixels des limites de chaque zone colorée dans le spectre. On utilisera pour cela la liste de longueurs d'ondes L, exprimées cette fois-ci en µm, du rendu colorimétrique de l'exercice précédent :
L=[0.38, 0.449, 0.466, 0.478, 0.483, 0.49, 0.51, 0.541, 0.573, 0.575, 0.579, 0.584, 0.588, 0.593, 0.605, 0.622, 0.7]
Un exemple d'exécution :
>>> px(L,30,3)
[500, 298, 262, 239, 229, 217, 184, 140, 102, 100, 96, 91, 87, 82, 70, 55, 0]
5. A l'aide des fonctions définies précédemment, créer un script permettant de représenter le spectre de la lumière blanche obtenue à l'aide de ce prisme. La liste de couleurs utilisée sera celle de l'exercice précédent :
color=[(15,0,36),(17,0,48),(0,18,51),(0,28,41),(0,32,38),(0,45,37),(0,69,42),(35,75,0),(79,70,0),(82,66,0),(84,58,0),(87,52,0),(91,47,0),(96,31,0),(92,0,13),(48,0,13)]
Un exemple d'exécution :


Le rendu des couleurs peut être amélioré en appliquant pour chaque tranche de longueur d'onde une approximation linéaire permettant de déterminer le triplet RVB correspondant à la couleur étudiée. Par exemple :
1. Définir une fonction RVB(lo) retournant un tuple (R,V,B) contenant les valeurs R, V et B obtenues à l'aide de l'algorithme précédent.
Quelques exemples d'exécution :
>>> RVB(710)
(157, 0, 0)
>>> RVB(400)
(60, 0, 91)
>>> RVB(550)
(145, 255, 0)
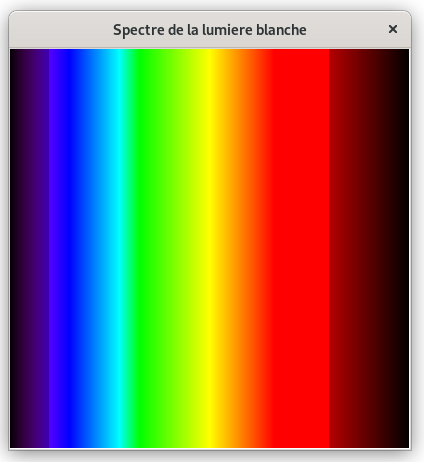
2. Créer un script dessinant dans une fenêtre de 400x400 pixels le spectre de la lumière blanche pour des longueurs d'onde comprises entre 380 et 780 nm. On utilisera comme échelle 1 pixel pour 1 nm selon l'axe x.
Un exemple d'exécution :

Le modèle de Bohr décrit l'atome d'hydrogène comme un noyau massif et chargé positivement, autour duquel se déplace un électron chargé négativement. Selon le premier postulat de la théorie de Bohr, l'électron ne rayonne aucune énergie lorsqu'il se trouve sur une orbite stable, supposée circulaire de rayon :
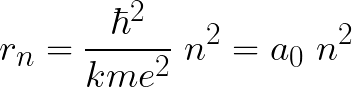
a0 est la plus petite valeur du rayon possible, on l'appelle rayon de Bohr et sa valeur est d'approximativement 53 pm.
k est la constante de Coulomb de valeur 9.109 N.m.C-2
1. Définir une fonction structure(Z) retournant une liste de trois entiers représentant le nombre d'électrons sur les couches K, L et M.
Des exemples d'exécution :
>>> structure(1)
[1, 0, 0]
>>> structure(3)
[2, 1, 0]
>>> structure(11)
[2, 8, 1]
2. Définir une fonction rayon(n) retournant la valeur en pm du rayon de l'orbite de Bohr en fonction de la valeur du nombre quantique principal n.
Un exemple d'exécution :
>>> rayon(3)
477
3. Définir une fonction positions(S) retournant une liste de tuples représentant les coordonnées (x,y) en pm des électrons répartis régulièrement sur leur orbite de Bohr pour une structure électronique S.
Rappel : l'abscisse x et l'ordonnée y d'un point M situé sur un cercle de rayon r et de centre O sont donné par les relations x=r*cos(theta) et y=r* sin(theta) où theta désigne l'angle ((Ox),OM).
Des exemples d'exécution :
>>> positions([1,0,0])
[(53, 0)]
>>> positions([2,1,0])
[(53, 0), (-53, 0), (212, 0)]
>>> positions([2,8,1])
[(53, 0), (-53, 0), (212, 0), (149, 149), (0, 212), (-149, 149), (-212, 0), (-149, -149), (0, -212), (149, -149), (477, 0)]
4. Créer un script demandant à l'utilisateur de saisir un numéro atomique Z et représentant dans une fenêtre de 500x500 pixels :
Aide : on utilisera pour afficher un disque de centre (px,py) et de rayon r en pixels la fonction disc(px,py,r).
Attention : il faut tenir compte de l'échelle 1/2 pour placer dans la fenêtre les électrons.
Des exemples d'exécution pour Z=1, Z=3 et Z=11 :
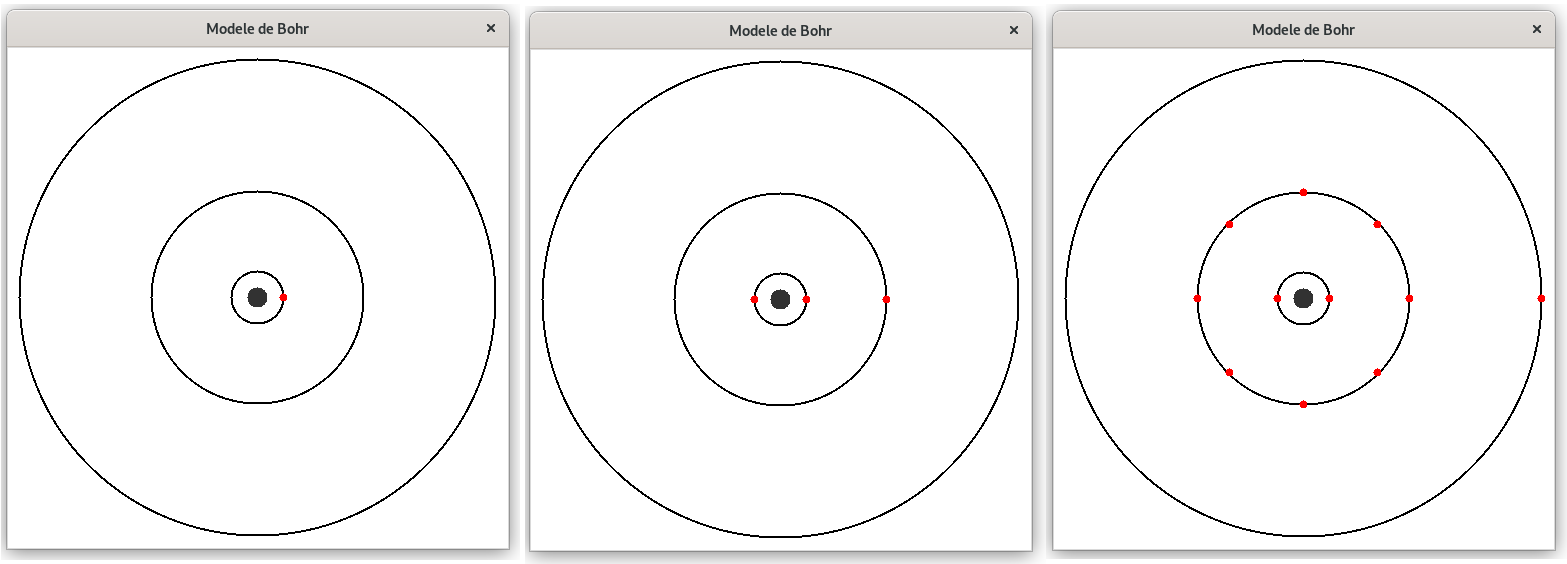

L'équation de Schrödinger permet, dans le cas de l'Hydrogène, de déterminer l'expression de la fonction d'onde associée à son unique électron.
Dans le cas de l'orbitale atomique 1s (pour laquelle n=1 et l=0) l'expression de cette fonction d'onde est :
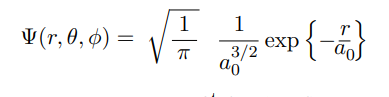
1. Définir une fonction psi2(r) permettant de calculer la valeur du carré de la fonction d'onde. On prendra comme valeur pour le rayon de Bohr a0=53 pm et on exprimera r en pm.
Des exemples d'exécution :
>>> psi2(0)
2.138072947357823e-06
>>> psi2(10)
1.4660129557267116e-06
>>> psi2(100)
4.911062000436052e-08
2. Créer un script permettant de tracer la courbe (en noir, d'épaisseur 2 avec 250 points) représentant la fonction d'onde psi2(r) à l'aide de pocketgl. La courbe sera affichée dans une fenêtre de dimension 250x500 pixels en utilisant l'échelle suivante : 1 pixel pour 1 pm en abscisse et 1 pixel pour 5e-9 en ordonnée.

3. Modifier votre script pour tracer en bleu un rectangle entre les points (r,0) et (r+10,psi2(r+10)) pour toutes les valeurs de r multiples de 10 pm.

4. Définir une fonction aire_psi2(r1,r2) permettant de calculer l'aire d'un des rectangles précédent représenté entre les points (r1,0) et (r2,psi2(r2)).
Des exemples d'exécution :
>>> aire_psi2(0,10)
2932.0259114534233
>>> aire_psi2(100,110)
67.34737959164185
5. Définir une fonction densite_probabilite() retournant une liste L ordonnée des valeurs de aire_psi2(r,r+1) pour des valeurs de r allant de 0 à 249.
6. Définir une fonction probabilite(L) retournant une liste L2 contenant les valeurs cumulées de la liste retournée par la fonction densite_probabilite(). Utiliser la dernière valeur de la liste pour renormaliser la liste c'est à pour s'assurer que le dernier élément de la liste L2 a pour valeur 1 ( ce qui revient à dire que l'électron est nécessairement présent dans notre fenêtre).
7. Créer un script permettant d'afficher dans une fenêtre de 500x500 pixels un repère orthonormé (O,x,y) centré au point (250,250).

8. Définir une fonction place_electron(L2) :
Aide : on utilisera pour générer un nombre aléatoire compris entre 0 et 1 la fonction random() de la bibliothèque random importée à l'aide de la ligne
from random import random
9. Modifier votre script pour qu'il demande à l'utilisateur un nombre N de positions de l'électron et place les N positions dans votre fenêtre.
 ...................
...................
 ...................
...................