Les fonctions sont des blocs d'instructions sortis du programme principal afin de limiter les répétitions d'instructions, assurer la modularité du code et améliorer sa lisibilité. On distingue généralement les fonctions assumant le rôle de fonction qui effectuent un calcul et retourne un résultat des fonctions assumant le rôle de procédure qui effectuent une suite de tâches particulières : dans le cas des procédures, il est courant de retourner un code d'erreur permettant simplement de vérifier que le bloc d'instructions s'est déroulée correctement.
Une fonction Python est définie par le spécificateur def suivi du nom de la fonction et de ses paramètres :
def nomDeLaFonction(liste de paramètres):
........
.....bloc d'instructions
........
.....return resultat
On peut choisir n'importe quel nom pour la fonction à l'exception des mots réservés du langage et à la condition de n'utiliser aucun caractère spécial ou accentué (le caractère souligné « _ » est permis).
L'instruction def est une instruction composée. La ligne contenant cette instruction se termine obligatoirement par un double point, lequel introduit un bloc d'instructions qu'il faut indenter.
La liste de paramètres représente les arguments du programme principal que la fonction doit utiliser pour retourner son résultat. Cette liste peut être vide.
Cette fonction "s'appelle" dans un programme à l'aide de son nom suivi de parenthèses contenant ou pas les arguments de la fonction.
Il est possible qu'une fonction ne renvoie pas de résultat, on parle dans ce cas de procédure.
Le type et la valeur de l'argument restent inchangés lors du passage à la fonction, ce qui ne signifie pas qu'ils le restent lors de l'exécution du programme...
1. Taper dans l'éditeur de fichier python le code suivant puis l'exécuter.
# définition de la fonction
def ma_fonction(x) :
.....print(x,x)
.....return "OK"
Taper ensuite dans un terminal python l'instruction suivante :
>>> ma_fonction("Bonjour")
Noter le résultat obtenu. Quelle(s) tâche(s) réalise la fonction "ma_fonction" ?
2. Taper dans l'éditeur de fichier python le code suivant puis l'exécuter.
# définition de la fonction
def ma_fonction(x) :
.....return 2*x+1
Taper ensuite dans un terminal python l'instruction suivante :
>>> ma_fonction(3)
Noter le résultat obtenu. Quelle tâche réalise cette fois-ci la fonction "ma_fonction" ?
3. Taper dans l'éditeur de fichier python le code suivant puis l'exécuter.
# définition de la fonction
def ma_fonction(x) :
.....return 2*x+1
# corps principal du programme
x=int(input("Entrer la valeur de x : "))
print("la valeur de ma fonction est :",ma_fonction(x))
4. Modifier le programme précédent pour qu'il puisse retourner une liste de valeurs associée à une suite de valeurs saisies au clavier par l'utilisateur.
Un exemple d'exécution :
Entrer une valeur de x (taper Q pour terminer): 1
Entrer une valeur de x (taper Q pour terminer): 2
Entrer une valeur de x (taper Q pour terminer): -1
Entrer une valeur de x (taper Q pour terminer): 3.14
Entrer une valeur de x (taper Q pour terminer): Q
la liste de valeurs de la fonction est : [3.0, 5.0, -1.0, 7.28]
Il est possible de tracer à l'aide de python des fonctions (qui renvoient un résultat numérique) en utilisant une bibliothèque graphique, comme par exemple matplotlib. Pour cela il faut d'abord importer en tout début du programme cette bibliothèque.
Par exemple, pour importer l'ensemble de fonctions pyplot (qui sert à tracer les fonctions) de la bibliothèque matplotlib il faut écrire en tout début de programme l'instruction :
from matplotlib import pyplot
1. Taper dans l'éditeur de fichier le code suivant puis l'exécuter :
from matplotlib import pyplot
# Donnees sous forme de deux listes, listeX pour les abscisses et listeY pour les ordonnees
listeX=[-1,1,2,3.14]
listeY=[-1,3,5,7.28]
# trace des points
pyplot.scatter(listeX,listeY,s=20,c='blue',marker='+',linewidth=1,label='Y=f(X)')
# legende des axes
pyplot.xlabel('X')
pyplot.ylabel('Y')
pyplot.legend()
# titre du graphique
pyplot.title("Mon graphique")
# affichage du graphique
pyplot.show()
A quoi servent les fonctions pyplot.scatter(), pyplot.xlabel(), pyplot.ylabel(), pyplot.legend(), pyplot.title(), pyplot.show() ?
2. Modifier les arguments autres que listeX et listeY de la fonction pyplot.scatter() et en déduire leur rôle.
3. Créer un programme permettant de représenter l'enregistrement à l'aide d'un micro d'une période temporelle d'un son pur de fréquence 440 Hz et d'amplitude 1 V. On utilisera pour cela la fonction sin() et la valeur pi importées de la bibliothèque math et on prendra 200 points pour une période.
Remarque : on calculera les 200 valeurs de listeX à l'aide d'une boucle de même que celles de listeY.
Un exemple d'exécution :
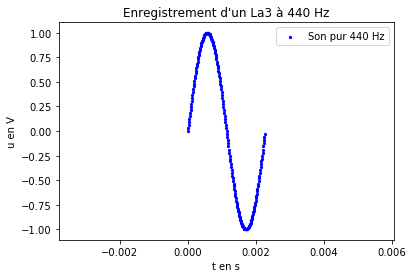
4. Il est possible de spécifier les limites des axes x et y à l'aide des fonctions pyplot.xlim(xmin, xmax) et pyplot.ylim(ymin,ymax) : modifier votre programme précédent pour qu'il affiche avec une étendue maximale la courbe précédente.
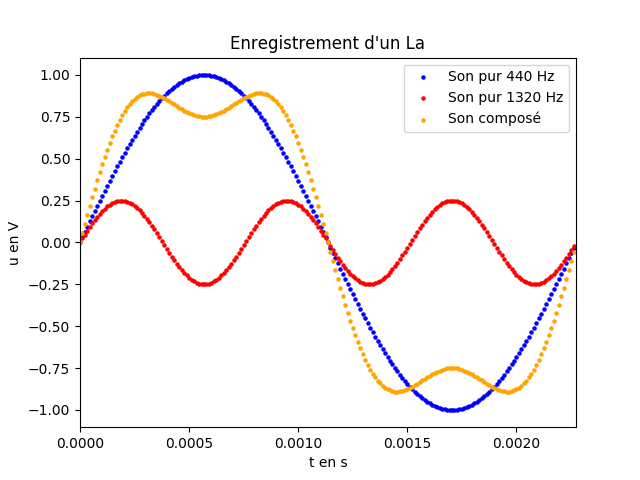
5. Créer un nouveau programme permettant de tracer les courbes correspondantes à deux sons purs de fréquence 440 Hz et 1320 Hz et d'amplitude respectives 1 V et 0.25 V ainsi que celle correspondant à la somme de ces deux sons purs.
Un exemple d'exécution :
La diffraction par une fente est un modèle théorique utilisé pour modéliser les phénomènes de diffraction en optique. Une fente est une ouverture de largeur a et de longueur infinie, centrée sur l'origine (la fente s'étend de -a/2 à a/2 sur l'axe des x). Du fait de la symétrie par translation du problème, on ne considère les variations d'intensité que sur un seul axe x. Dans le cas où l'écran est situé assez loin, on peut considérer que les rayons qui arrivent en un point M sont parallèles. Dans ce cas, l'intensité lumineuse en un point d'abscisse x de l'écran s'écrit :
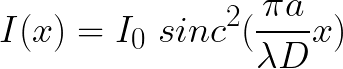..... avec .....
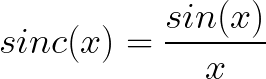
1. Définir la fonction sinus_cardinal(x).
ATTENTION : cette fonction doit pour x=0 renvoyer la valeur 1.
Des exemples d'exécution :
>>> sinus_cardinal(0)
1
>>> sinus_cardinal(1)
0.8414709848078965
2. Définir la fonction intensite(a,x,lo,D) qui a pour arguments la largeur de la fente notée a, la longueur d'onde notée lo (le mot lambda est un mot réservé du langage python), la distance à la source D et l'abscisse x du point M.
Remarque : on fixera l'intensité en x=0 à la valeur 1 cd.
Un exemple d'exécution :
>>> intensite(0.5e-3,3e-2,650e-9,3)
0.00115976394091804
3. Créer le script permettant de représenter la courbe correspondant à l'intensité lumineuse d'une figure de diffraction lors de la diffraction par une fente d'une onde lumineuse de longueur d'onde donnée.
Il doit permettre à l'utilisateur de saisir :
Remarque : on calculera 1000 valeurs pour la liste d'abscisses listeX ainsi que pour la liste des ordonnées listeY.
Un exemple d'exécution :
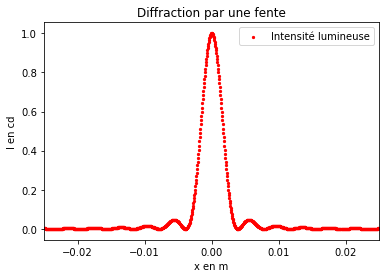
4. Modifier votre script pour calculer aussi la largeur de la tache centrale.
Aide : la largeur de la tache centrale est donnée ici par la formule : L = 2*lo*D/a
Un exemple d'exécution (la courbe obtenue n'est pas modifiée et n'a donc pas été recopiée ci-dessous) :
-------------------------
Diffraction par une fente
-------------------------
Entrez la largeur de la fente a en m : 0.5e-3
Entrez la longueur d'onde lambda en m: 650e-9
Entrez la distance entre la fente et l'ecran D en m: 3
Entrez la valeur minimale de x en m: -2.5e-2
Entrez la valeur maximale de x en m: 2.5e-2
La largeur de la tache centrale est : 0.0078 m
Un vecteur u(u1, u2 , u3, ...) dans un espace à n dimensions peut être représenté par une liste de n composantes réelles : on utilisera dans cet exercice la structure de données tuple pour représenter un vecteur. Par exemple pour un vecteur u ayant 3 composantes réelles 1.0, 0 et 3.0, la variable correspondante sera u=(1.0,0,3.0).
1. Définir une fonction saisie_vecteur() qui demande la saisie d'un vecteur à l'utilisateur coordonnées par coordonnées et retourne un tuple contenant les coordonnées saisies. La fonction affichera de plus "OK, vecteur à n dimensions enregistré" où n est automatiquement remplacé par le nombre de coordonnées du vecteur.
Un exemple d'exécution :
>>> saisie_vecteur()
Entrer la valeur de la coordonnee (Q pour quitter) : 1
Entrer la valeur de la coordonnee (Q pour quitter) : 2
Entrer la valeur de la coordonnee (Q pour quitter) : 1
Entrer la valeur de la coordonnee (Q pour quitter) : Q
OK, vecteur a 3 dimensions enregistre
(1.0, 2.0, 1.0)
2. Définir une fonction somme(u,v) qui calcule et retourne sous la forme d'un tuple la somme de deux vecteurs u et v donnés en paramètres. Cette fonction doit pouvoir être utilisée quel que soit le nombre (identique) de coordonnées des deux vecteurs.
Un exemple d'exécution :
>>> somme((1,1,1),(-1,0,1))
(0, 1, 2)
3. Définir une fonction mult(a,u) qui calcule et retourne le produit du vecteur u par le réel a.
Un exemple d'exécution :
>>> mult(2,(-1,0,1))
(-2, 0, 2)
4. Ecrire un script affichant le résultat de a*u+b*v où a, b sont des réels donnés par l’utilisateur ainsi que u et v des vecteurs saisis coordonnée par coordonnée.
Un exemple d'exécution :
------------------------------
Programme de calcul de a*u+b*v
------------------------------
Saisie du vecteur u
Entrer la valeur de la coordonnee (Q pour quitter) : 1
Entrer la valeur de la coordonnee (Q pour quitter) : 2
Entrer la valeur de la coordonnee (Q pour quitter) : 1
Entrer la valeur de la coordonnee (Q pour quitter) : Q
OK, vecteur a 3 dimensions enregistre
Saisie du vecteur v
Entrer la valeur de la coordonnee (Q pour quitter) : 4
Entrer la valeur de la coordonnee (Q pour quitter) : 1
Entrer la valeur de la coordonnee (Q pour quitter) : -1
Entrer la valeur de la coordonnee (Q pour quitter) : Q
OK, vecteur a 3 dimensions enregistre
Entrez la valeur de a : 2
Entrez la valeur de b: 3
Le resultat est : (14.0, 7.0, -1.0)
5. Définir une fonction produit_scalaire(u,v) qui calcule et retourne le produit scalaire de deux vecteurs u et v de même dimension donnés en paramètres puis écrire un script calculant le produit scalaire de deux vecteurs saisis par l'utilisateur coordonnée par coordonnée.
Un exemple d'exécution :
------------------------------------------
Programme de calcul du produit scalaire uv
------------------------------------------
Saisie du vecteur u
Entrer la valeur de la coordonnee (Q pour quitter) : 1
Entrer la valeur de la coordonnee (Q pour quitter) : 2
Entrer la valeur de la coordonnee (Q pour quitter) : 1
Entrer la valeur de la coordonnee (Q pour quitter) : Q
OK, vecteur a 3 dimensions enregistre
Saisie du vecteur v
Entrer la valeur de la coordonnee (Q pour quitter) : 4
Entrer la valeur de la coordonnee (Q pour quitter) : 2
Entrer la valeur de la coordonnee (Q pour quitter) : -1
Entrer la valeur de la coordonnee (Q pour quitter) : Q
OK, vecteur a 3 dimensions enregistre
Le produit scalaire vaut : 7.0
6. Définir la fonction norme(u) qui calcule et retourne la norme du vecteur u donné en paramètre puis écrire un script calculant la norme d'un vecteur saisis par l'utilisateur coordonnée par coordonnée.
Un exemple d'exécution :
--------------------------------------------
Programme de calcul de la norme d'un vecteur
--------------------------------------------
Saisie du vecteur u
Entrer la valeur de la coordonnee (Q pour quitter) : 1
Entrer la valeur de la coordonnee (Q pour quitter) : 2
Entrer la valeur de la coordonnee (Q pour quitter) : 1
Entrer la valeur de la coordonnee (Q pour quitter) : Q
OK, vecteur a 3 dimensions enregistre
La norme vaut : 2.449489742783178
7. Définir la fonction cosinus(u,v) qui calcule et retourne le cosinus de l’angle (u,v) puis écrire un script calculant le cosinus de l'angle(u,v) à l'aide de deux vecteurs saisis par l'utilisateur coordonnée par coordonnée.
On rappelle la définition du cosinus de l’angle (u,v) :
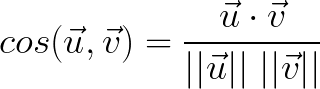
Un exemple d'exécution :
-----------------------------------------------
Programme de calcul du cosinus de l'angle (u,v)
-----------------------------------------------
Saisie du vecteur u
Entrer la valeur de la coordonnee (Q pour quitter) : 1
Entrer la valeur de la coordonnee (Q pour quitter) : 2
Entrer la valeur de la coordonnee (Q pour quitter) : 1
Entrer la valeur de la coordonnee (Q pour quitter) : Q
OK, vecteur a 3 dimensions enregistre
Saisie du vecteur v
Entrer la valeur de la coordonnee (Q pour quitter) : 4
Entrer la valeur de la coordonnee (Q pour quitter) : 2
Entrer la valeur de la coordonnee (Q pour quitter) : -1
Entrer la valeur de la coordonnee (Q pour quitter) : Q
OK, vecteur a 3 dimensions enregistre
Le cosinus de l'angle (u,v) vaut : 0.6236095644623236
La fonction exponentielle peut être développée en série entière de la manière suivante :
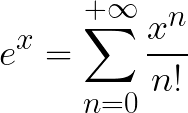
Le cas x=1 donnant alors la valeur de la constante e:
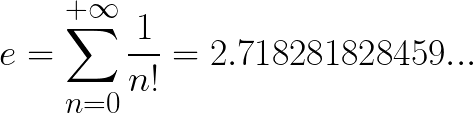
1. Définir la fonction factorielle(n) qui retourne n!.
Rappel : en mathématiques, la fonction factorielle est définie par :
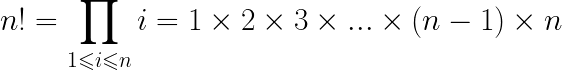
avec comme cas de base 0!=1
Des exemples d'exécution :
>>> factorielle(0)
1
>> factorielle(1)
1
>>> factorielle(2)
2
>>> factorielle(3)
6
>>> factorielle(12)
479001600
2. Définir la fonction puissance(x,n) qui retourne x puissance n où x est un réel et n un entier.
Des exemples d'exécution :
>>> puissance(0,0)
1
>>> puissance(10,0)
1
>>> puissance(2,8)
256
>>> puissance(3.14,2)
9.8596
3. Définir une fonction serie_exp(x,n) qui retourne la valeur de l'exponentielle développée en série entière pour x et n donnés.
Un exemple d'exécution :
>>> serie_exp(1,4)
2.708333333333333
4. Écrire un script qui demande un flottant x à l’utilisateur puis une précision entière p qui affiche la valeur de l'exponentielle ainsi que la plus petite valeur n telle que :
On comparera pour cela la valeur de l'exponentielle obtenue à l'aide de la série entière et celle obtenue par la fonction exp(x) de la bibliothèque math.
Remarque : on peut utiliser pour arrondir la valeur trouvée la fonction python prédéfinie round(x,p)
Un exemple d'exécution :
Entrez la valeur de x : 1
Entrez la precision entiere p : 4
La valeur de l'exponentielle est: 2.7183
La plus petite valeur de n possible pour avoir cette precision est : 7